Cdtjkyj

Pour les articles homonymes, voir Identité.

Représentation graphique de l'identité remarquable (a+b)3=a3+3a2b+3ab2+b3{displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}}.

En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités^[évasif] qui s'appliquent à des nombres, ou plus généralement à des variables polynomiales. Elles servent en général à accélérer les calculs, à simplifier certaines écritures, à factoriser ou à développer des expressions. Elles servent pour la résolution des équations du second degré et sont plus généralement utiles pour la recherche de solutions d'équations^{[Note 1]}.

La plupart de ces identités remarquables ont tout d'abord été démontrées à l'aide de raisonnements géométriques, puis ont été généralisées à des puissances supérieures par des calculs algébriques.

Identités remarquables du second degré |

Dans toute la suite, a et b désignent des nombres, qui peuvent être des entiers, des rationnels et réels, ou même des complexes. Ces identités sont vraies plus généralement dans un anneau commutatif, ou même dans un anneau quelconque où a et b commutent.

Énoncés |

Les trois identités remarquables du second degré sont^[1] :

La deuxième de ces identités peut être vue comme un cas particulier de la première, en prenant, au lieu de b, –b dans la première égalité. Ces égalités font l'objet d'un vocabulaire spécifique :

Définition d'un produit remarquable^[1] — Les trois expressions suivantes sont appelées produit remarquable :

(a+b)2,(a−b)2et(a+b)(a−b).{displaystyle (a+b)^{2},quad (a-b)^{2}quad {text{et}}quad (a+b)(a-b).}

On définit de même :

Définition d'une somme remarquable^[1] — Les trois expressions suivantes sont appelées somme remarquable :

a2+2ab+b2,a2−2ab+b2eta2−b2.{displaystyle a^{2}+2ab+b^{2},quad a^{2}-2ab+b^{2}quad {text{et}}quad a^{2}-b^{2}.}

Exemples |

Développement et réduction |

Les identités remarquables permettent de transformer l'écriture de certaines expressions algébriques, comme dans l'exemple suivant^[2] :

A=(2x−3)2+(x+5)(3−x).{displaystyle A=(2x-3)^{2}+(x+5)(3-x).}

L'expression A est la somme de deux termes. Le premier terme est un produit remarquable, que l'on peut transformer en somme :

(2x−3)2=(2x)2−2×2x×3+32=4x2−12x+9etA=4x2−12x+9+(x+5)(3−x).{displaystyle (2x-3)^{2}=(2x)^{2}-2times 2xtimes 3+3^{2}=4x^{2}-12x+9quad {text{et}}quad A=4x^{2}-12x+9+(x+5)(3-x).}

Le deuxième terme se traite à l'aide de la distributivité de la multiplication par rapport à l'addition :

(x+5)(3−x)=x(3−x)+5(3−x)=3x−x2+15−5x=−x2−2x+15.{displaystyle (x+5)(3-x)=x(3-x)+5(3-x)=3x-x^{2}+15-5x=-x^{2}-2x+15.}

En additionnant termes à termes, on obtient :

Équation du second degré |

Les identités remarquables permettent de résoudre une équation du second degré. Illustrons la méthode sur l'exemple suivant :

x2+2x−5=0.{displaystyle x^{2}+2x-5=0.}

La méthode consiste à travailler la partie de l'expression qui ne dépend pas de x de manière à utiliser une des deux premières identités remarquables et factoriser la partie qui dépend de x :

x2+2x−5=x2+2x+1−6.{displaystyle x^{2}+2x-5=x^{2}+2x+1-6.}

Les trois premiers termes sont maintenant une somme remarquable, il est possible d'appliquer une identité remarquable et l'équation devient :

x2+2x−5=(x+1)2−6=(x+1)2−(6)2=0.{displaystyle x^{2}+2x-5=(x+1)^{2}-6=(x+1)^{2}-({sqrt {6}})^{2}=0.}

On reconnaît une nouvelle somme remarquable, l'équation s'écrit encore :

x2+2x−5=(x+1+6)(x+1−6)=0.{displaystyle x^{2}+2x-5=(x+1+{sqrt {6}})(x+1-{sqrt {6}})=0.}

Un produit a.b de deux nombres a et b est nul si, et seulement si, a ou b est nul^{[Note 2]}. Résoudre l'équation revient à résoudre deux équations du premier degré :

(1)x+1+6=0et(2)x+1−6=0.{displaystyle (1);x+1+{sqrt {6}}=0quad {text{et}}quad (2);x+1-{sqrt {6}}=0.}

On trouve les deux solutions de l'équation, appelées aussi racines du polynôme :

La même méthode, appliquée à des coefficients a{displaystyle a}, b{displaystyle b}, et c{displaystyle c} (ax2+bx+c=0{displaystyle ax^{2}+bx+c=0}) au lieu des coefficients 1, 2, et –5 de l'exemple précédent, fait apparaitre le rôle du discriminant et les deux solutions.

Polynômes au carré |

Pour élever au carré un polynôme avec un nombre quelconque de termes, ajouter les carrés de chaque terme individuellement, puis ajouter le double de la somme des produits de chaque paire possible de termes.

(a+b+c)2=a2+b2+c2+2(ab+ac+bc),{displaystyle (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+ac+bc),}

(a+b+c+d)2=a2+b2+c2+d2+2(ab+ac+ad+bc+bd+cd).{displaystyle (a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(ab+ac+ad+bc+bd+cd).}

Identité remarquable et géométrie |

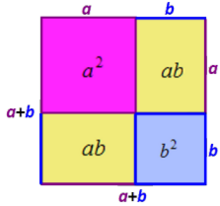
Ces identités remarquables sont connues depuis les Babyloniens^[3]. Il est possible qu'ils se soient rendu compte de ces égalités à l'aide de raisonnements géométriques. Il existe une méthode simple pour trouver la formule suivante^{[Note 3]} :

(a+b)2=a2+2ab+b2.{displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}.}

La figure de droite représente un carré. On suppose que la longueur du côté du carré rose est égale à a et celle du carré bleu à b. L'aire du grand carré est égale à (a + b)².

Il existe une autre manière d'exprimer cette aire : elle est la somme des aires des zones rose, bleue et des deux zones jaunes. L'aire rose est égale à a² car c'est un carré de côté a, l'aire bleue est égale à b², et chacune des deux aires jaunes est égale à ab car c'est un rectangle de côtés a et b. On obtient bien la formule annoncée.

Démonstration par l'algèbre |

L'algèbre permet encore de démontrer ces formules. Calculons (a - b)². La distributivité montre que :

(a−b)2=(a−b)(a−b)=a(a−b)−b(a−b)=a2−ab−ba+b2=a2−2ab+b2.{displaystyle (a-b)^{2}=(a-b)(a-b)=a(a-b)-b(a-b)=a^{2}-ab-ba+b^{2}=a^{2}-2ab+b^{2}.}

On démontre de même la troisième identité remarquable :

(a+b)(a−b)=a(a−b)+b(a−b)=a2−ab+ba−b2=a2−b2.{displaystyle (a+b)(a-b)=a(a-b)+b(a-b)=a^{2}-ab+ba-b^{2}=a^{2}-b^{2}.}

Identités remarquables diverses |

Identité de Brahmagupta |

Brahmagupta, un mathématicien indien du VI^e siècle découvre une identité remarquable du quatrième degré^[4] :

(a2−nb2)(c2−nd2)=(ac+nbd)2−n(ad+bc)2.{displaystyle (a^{2}-nb^{2})(c^{2}-nd^{2})=(ac+nbd)^{2}-n(ad+bc)^{2}.}

Il l'utilise dans le cas où a, b, c, d et n sont des nombres entiers. Elle permet de calculer une bonne approximation d'une racine carrée.

Application au calcul de √3

Brahmagupta remarque que 2² - 3.1² = 1. Il applique son identité plusieurs fois, toujours avec n = 3. La première fois, il pose a = c = 2, b = d = 1. Il obtient :

(22−3⋅1)(22−3⋅1)=(2⋅2+3⋅1)2−3(2⋅1+1⋅2)2=72−3⋅42=1.{displaystyle (2^{2}-3cdot 1)(2^{2}-3cdot 1)=(2cdot 2+3cdot 1)^{2}-3(2cdot 1+1cdot 2)^{2}=7^{2}-3cdot 4^{2}=1.}

Il recommence avec cette fois avec : a = c = 7, b = d = 4. Il obtient une nouvelle manière d'écrire 1 :

972−3⋅562=1.{displaystyle 97^{2}-3cdot 56^{2}=1.}

Il réapplique la même logique, il obtient encore une autre manière d'écrire 1 :

188172−3⋅108642=1.{displaystyle 18,817^{2}-3cdot 10,864^{2}=1.}

Cette égalité s'écrit encore :

188172=3⋅108642+1et(1881710864)2=3+1108642.{displaystyle 18,817^{2}=3cdot 10,864^{2}+1quad {text{et}}quad left({frac {18,817}{10,864}}right)^{2}=3+{frac {1}{10,864^{2}}}.}

Il obtient une fraction dont le carré est « presque » égal à 3, ce qui revient à dire que 18 817/10 864 est « presque » égal à √3. Si on calcule la fraction, on trouve un résultat dont les neuf premiers chiffres significatifs fournissent la meilleure approximation possible (avec le même nombre de décimales), à savoir : 1,73205081.

Il utilise aussi sa formule pour trouver des solutions à l'équation diophantienne dite de Pell-Fermat.

Identité des quatre carrés d'Euler |

L'identité des quatre carrés d'Euler relie entre eux huit nombres. Elle prend la forme suivante :

(a12+a22+a32+a42)(b12+b22+b32+b42){displaystyle (a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2})(b_{1}^{2}+b_{2}^{2}+b_{3}^{2}+b_{4}^{2})}

=(a1b1−a2b2−a3b3−a4b4)2+(a1b2+a2b1+a3b4−a4b3)2{displaystyle =(a_{1}b_{1}-a_{2}b_{2}-a_{3}b_{3}-a_{4}b_{4})^{2}+(a_{1}b_{2}+a_{2}b_{1}+a_{3}b_{4}-a_{4}b_{3})^{2}}

+(a1b3−a2b4+a3b1+a4b2)2+(a1b4+a2b3−a3b2+a4b1)2.{displaystyle +,(a_{1}b_{3}-a_{2}b_{4}+a_{3}b_{1}+a_{4}b_{2})^{2}+(a_{1}b_{4}+a_{2}b_{3}-a_{3}b_{2}+a_{4}b_{1})^{2}.}

Elle est utilisée, entre autres pour démontrer le théorème des quatre carrés qui indique que tout nombre entier est somme de quatre carrés.

Identité de Sophie Germain |

L'identité de Sophie Germain énonce que pour tous nombres x et y, on a :

x4+4y4=(x2+2y2)2−4x2y2=(x2+2y2−2xy)(x2+2y2+2xy)=((x+y)2+y2)((x−y)2+y2).{displaystyle x^{4}+4y^{4}=(x^{2}+2y^{2})^{2}-4x^{2}y^{2}=(x^{2}+2y^{2}-2xy)(x^{2}+2y^{2}+2xy)=((x+y)^{2}+y^{2})((x-y)^{2}+y^{2}).}

Identité d'Argand |

(x2+x+1)(x2−x+1)=x4+x2+1.{displaystyle (x^{2}+x+1)(x^{2}-x+1)=x^{4}+x^{2}+1.}

Identité de Gauss |

a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−ac−bc)=12(a+b+c)[(a−b)2+(b−c)2+(a−c)2].{displaystyle a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-ac-bc)={frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}].}

Identités de Legendre |

(a+b)2+(a−b)2=2(a2+b2),{displaystyle (a+b)^{2}+(a-b)^{2}=2(a^{2}+b^{2}),}

(a+b)2−(a−b)2=4ab,{displaystyle (a+b)^{2}-(a-b)^{2}=4ab,}

(a+b)4−(a−b)4=8ab(a2+b2).{displaystyle (a+b)^{4}-(a-b)^{4}=8ab(a^{2}+b^{2}).}

Identités de Lagrange |

(a2+b2)(x2+y2)=(ax+by)2+(ay−bx)2,{displaystyle (a^{2}+b^{2})(x^{2}+y^{2})=(ax+by)^{2}+(ay-bx)^{2},}

(a2+b2+c2)(x2+y2+z2)=(ax+by+cz)2+(ay−bx)2+(az−cx)2+(bz−cy)2.{displaystyle (a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})=(ax+by+cz)^{2}+(ay-bx)^{2}+(az-cx)^{2}+(bz-cy)^{2}.}

La première identité de Lagrange ici listée est un cas particulier de l'identité de Brahmagupta.

Identités remarquables de degré n |

Formule du binôme de Newton |

La même technique de démonstration que celle utilisée pour les formules de degré 2 montre que, si a et b désignent toujours deux nombres :

(a+b)3=a3+3a2b+3ab2+b3,{displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3},}

(a−b)3=a3−3a2b+3ab2−b3.{displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}.}

Appliqué encore une fois, on obtient :

(a+b)4=a4+4a3b+6a2b2+4ab3+b4,{displaystyle (a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4},}

(a−b)4=a4−4a3b+6a2b2−4ab3+b4.{displaystyle (a-b)^{4}=a^{4}-4a^{3}b+6a^{2}b^{2}-4ab^{3}+b^{4}.}

De même,

(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5,{displaystyle (a+b)^{5}=a^{5}+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5},}

(a−b)5=a5−5a4b+10a3b2−10a2b3+5ab4−b5.{displaystyle (a-b)^{5}=a^{5}-5a^{4}b+10a^{3}b^{2}-10a^{2}b^{3}+5ab^{4}-b^{5}.}

On peut la généraliser à un degré n quelconque, à l'aide de la formule du binôme :

(x+y)n=∑k=0n(nk)xn−kyk.{displaystyle (x+y)^{n}=sum _{k=0}^{n}{n choose k}x^{n-k}y^{k}.}

Les coefficients de l'expression, considérée comme un polynôme en x et en y sont appelés coefficients binomiaux. Comme y peut prendre une valeur négative, on obtient bien les deux formes précédentes.

La formule s'applique même si x et y ne sont pas des nombres. Ces lettres peuvent désigner deux matrices qui commutent entre elles. De manière générale, la formule est vraie dans un anneau (supposé unitaire, c'est-à-dire. muni d'un élément unité 1=x0{displaystyle 1=x^{0}} pour tout x), si x et y commutent (ce qui est le cas en particulier si x ou y est égal à 1).

Différence ou somme de puissances |

Il est aussi possible de généraliser la troisième identité remarquable du second degré. Si a et b désignent deux nombres :

a3−b3=(a−b)(a2+ab+b2).{displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2}).}

a3+b3=(a+b)(a2−ab+b2),{displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2}),}

La formule suivante permet de généraliser la démarche. Tout d'abord, pour tout entier n ≥ 2,

an−bn=(a−b)(an−1+an−2b+⋯+abn−2+bn−1)=(a−b)∑k=0n−1an−1−kbk.{displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+cdots +ab^{n-2}+b^{n-1})=(a-b)sum _{k=0}^{n-1}a^{n-1-k}b^{k}.}

Cette formule a plusieurs applications importantes, comme une preuve que la fonction puissance est continue, ou la factorisation d'un polynôme à partir d'une racine. On a de plus, si n est impair,

an+bn=(a+b)(an−1−an−2b+⋯−abn−2+bn−1)=(a+b)∑k=0n−1(−1)kan−1−kbk.{displaystyle a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+cdots -ab^{n-2}+b^{n-1})=(a+b)sum _{k=0}^{n-1}(-1)^{k}a^{n-1-k}b^{k}.}

On a par ailleurs :

a4+b4=(a2+ab2+b2)(a2−ab2+b2).{displaystyle a^{4}+b^{4}=(a^{2}+ab{sqrt {2}}+b^{2})(a^{2}-ab{sqrt {2}}+b^{2}).}

Si l'on travaille dans un ensemble qui n'est pas celui des nombres, la dernière formule n'est valable que si √2 existe, c'est-à-dire s'il existe une valeur c telle que c² soit égal à 1 + 1. Il faut pour cela, en premier lieu, que l'élément neutre 1 de la multiplication existe.

Annexes |

Article connexe |

Livre II des Éléments d'Euclide

Liens externes |

• 
  Identités remarquables de degré supérieur à 2, sur le site de G. Villemin


• 
  Identités remarquables (Flash), sur le site de Sésamath
  

Bibliographie |

• 
  R. Brault, Mathématiques 3^e, Hachette éducation, 2008(ISBN 978-2-01-125539-6) — La première partie de l'article s'inspire largement de cette référence.


• 
  (en) Leonard Eugene Dickson, History of the Theory of Numbers (en) [détail des éditions], vol. II, Diophantine analysis — Les deux identités remarquables, ainsi que leurs usages en arithmétique sont présents dans cette référence, beaucoup plus technique que la précédente.

Notes |

Références |

• Portail de l’algèbre