Cdtjkyj

Pour le film de 1952, voir Arithmétique (film).

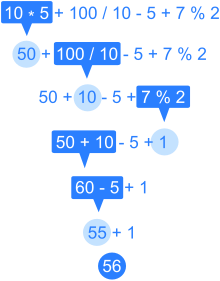
Illustration d’une décomposition arborescente d’un calcul arithmétique faisant intervenir l’addition (symbole +), la soustraction (symbole -), la multiplication (symbole *), le quotient (symbole /) et le reste (symbole %) de la division euclidienne.

L'arithmétique est une branche des mathématiques qui étudie la science des nombres^[1].

L'arithmétique s'est au départ limitée à l'étude des propriétés des entiers naturels, des entiers relatifs et des nombres rationnels (sous forme de fractions), et aux propriétés des opérations sur ces nombres. Les opérations arithmétiques traditionnelles sont l'addition, la division, la multiplication, et la soustraction. Cette discipline fut ensuite élargie par l'inclusion de l'étude d'autres nombres comme les réels (sous forme de développement décimal illimité), ou même de concepts plus avancés, comme l'exponentiation ou la racine carrée. Une arithmétique est une manière de représenter formellement - autrement dit, « coder » - les nombres (sous la forme d'une liste de chiffres, par exemple) ; et (grâce à cette représentation) définir les opérations de base : addition, multiplication, etc.

Histoire |

Allégorie de l'arithmétique.

L'étymologie du mot arithmétique est basée sur le grec ancien ἀριθμός (arithmos), qui signifie nombre^[2].

L’origine de l'arithmétique semble être une invention phénicienne^[3]. Dans l'école pythagoricienne, à la deuxième moitié du VI^e siècle av. J.-C., l'arithmétique était, avec la géométrie, l'astronomie et la musique, une des quatre sciences quantitatives ou mathématiques (Mathemata). Celles-ci furent regroupées au sein des sept arts libéraux par Martianus Capella (V^e siècle) et plus précisément désignées sous le nom de quadrivium par Boèce. Les trois autres disciplines étaient littéraires (grammaire, rhétorique, dialectique) et firent l'objet des travaux de Cassiodore et, plus tard, Alcuin qui leur donna le nom de trivium.

Différentes arithmétiques |

Arithmétique élémentaire |

L'expression « arithmétique élémentaire » désigne parfois la forme la plus basique des mathématiques, apprise à l’école élémentaire. Il s’agit essentiellement de l'étude des nombres et des opérations élémentaires (soustraction, addition, division, multiplication).

Ce terme désigne aussi les rudiments des techniques de l'arithmétique. Les outils utilisés sont la division euclidienne, le lemme d'Euclide, le théorème de Bachet-Bézout ou encore le théorème fondamental de l'arithmétique. Ils permettent de démontrer des théorèmes comme celui de Wilson ou encore le petit théorème de Fermat.

Cette deuxième acception du terme est traitée dans l'article détaillé.

Arithmétique modulaire |

Carl Friedrich Gauss (1777-1855) étudie l'ensemble des classes de congruence des entiers relatifs modulo un entier donné. Chaque classe correspond à un reste de la division euclidienne par cet entier, et l'ensemble est naturellement muni d'une addition et d'une multiplication.

L'étude de cette structure porte le nom d'arithmétique modulaire. Elle permet de généraliser les résultats de l'arithmétique élémentaire. Le théorème d'Euler, correspondant à un résultat plus fort que celui du petit théorème de Fermat, illustre une généralisation.

L'arithmétique modulaire est utilisé en cryptologie ou pour la construction de codes correcteurs en informatique.

Théorie algébrique des nombres |

De nombreuses questions ne trouvent pas de réponse, même avec les techniques de l'arithmétique modulaire. Des exemples proviennent d'équations diophantiennes, c'est-à-dire d'équations dont les coefficients sont entiers et dont les solutions recherchées sont entières. Une méthode consiste à élargir l'ensemble des entiers à une nouvelle structure qualifiée d'anneau d'entiers algébriques, comme celui des entiers de Gauss.

L'étude de ces structures, plus générales que celles de l'arithmétique modulaire qui se limite aux anneaux euclidiens, constitue le premier chapitre de la théorie algébrique des nombres.

Arithmétique des polynômes |

L'étude de l'arithmétique, au sens des nombres entiers, suppose d'établir des théorèmes. Ces théorèmes se démontrent à l'aide de techniques qui ne se limitent pas aux nombres entiers. Il est possible de faire usage de la même démarche sur d'autres structures, comme celle des polynômes. À travers l'étude des polynômes cyclotomiques, Gauss parvient à trouver un nouveau polygone régulier constructible à la règle et au compas, de 17 côtés.

Sa démarche est de nature arithmétique, pour cette raison, on parle d'arithmétique des polynômes.

Ensembles utilisés en arithmétique |

La totalité des nombres a été subdivisée en divers ensembles. Les plus connus sont :

• 
  N{displaystyle mathbb {N} } : l'ensemble des entiers naturels (0;1;2;3;4;5; etc.{displaystyle 0;,1;,2;,3;,4;,5;{mbox{ etc.}}}).


• 
  Z{displaystyle mathbb {Z} } : l'ensemble des entiers relatifs (−12;−2;0;5;6; etc.{displaystyle -12;,-2;,0;,5;,6;{mbox{ etc.}}}).


• 
  D{displaystyle mathbb {D} } : l'ensemble des nombres décimaux, c'est-à-dire qui s'écrivent sous la forme d'un quotient d'un nombre entier relatif et d'une puissance positive de 10, c'est-à-dire, x10n{displaystyle {frac {x}{10^{n}}}} où x est un nombre entier relatif et n un nombre entier naturel (−510,0,13100,1010{displaystyle {tfrac {-5}{10}},,0,,{tfrac {13}{100}},,{tfrac {10}{10}}}, etc.).
  


• 
  Q{displaystyle mathbb {Q} } : l'ensemble des nombres rationnels, c'est-à-dire des nombres pouvant s'écrire comme un quotient (résultat d'une division) de deux nombres entiers relatifs. En posant la division, il peut y avoir une infinité de chiffres après la virgule dans le résultat, mais ces chiffres finiront par se répéter ; dans ce cas on dit que l'écriture décimale est illimitée périodique (13;−513;227 etc.){displaystyle left({1 over 3};,-{5 over 13};{22 over 7}{mbox{ etc.}}right)}.


• 
  R{displaystyle mathbb {R} } : l'ensemble des nombres réels, mesurant toutes les distances entre deux points d'une droite, pouvant se voir comme limites de nombres rationnels, et pouvant s'écrire avec des chiffres après la virgule mais les chiffres ne se répètent plus nécessairement (π{displaystyle pi }, 2{displaystyle {sqrt {2}}}, etc.).


• 
  C{displaystyle mathbb {C} } : nombres complexes de la forme x+iy{displaystyle x+iy} où x et y sont réels et i{displaystyle i} imaginaire tel que i2=−1{displaystyle i^{2}=-1}.

Certains de ces ensembles sont des sous-ensembles des autres ; tous les éléments de N{displaystyle mathbb {N} } appartiennent aussi à Z{displaystyle mathbb {Z} }, par exemple. Mais à l'inverse, un élément de Q{displaystyle mathbb {Q} } n'est pas forcément élément de Z{displaystyle mathbb {Z} }. On peut représenter ces ensembles par des cercles concentriques : le plus petit est N{displaystyle mathbb {N} }, puis viennent Z{displaystyle mathbb {Z} }, D{displaystyle mathbb {D} }, Q{displaystyle mathbb {Q} }, R{displaystyle mathbb {R} } et C{displaystyle mathbb {C} }.

Il est possible de ne considérer qu'une partie d'un ensemble. Ainsi, on note R+{displaystyle mathbb {R} _{+}} l'ensemble des nombres positifs de R{displaystyle mathbb {R} }. De même on note R∗{displaystyle mathbb {R} ^{*}} l'ensemble R{displaystyle mathbb {R} } privé de 0. On remarque entre autres que Z+=N{displaystyle mathbb {Z} _{+}=mathbb {N} } et que Z∖N=Z−∗{displaystyle mathbb {Z} setminus mathbb {N} =mathbb {Z} _{-}^{*}} (il s'agit de Z{displaystyle mathbb {Z} } « privé de » N{displaystyle mathbb {N} }).

Propriétés |

De nombreux nombres entiers ont des propriétés particulières. Ces propriétés font l'objet de la théorie des nombres. Parmi ces nombres particuliers, les nombres premiers sont sans doute les plus importants.

Nombres premiers |

C'est le cas des nombres dits premiers. Ce sont les entiers naturels possédant uniquement deux diviseurs positifs distincts, à savoir 1 et eux-mêmes. Les dix premiers nombres premiers sont 2, 3, 5, 7, 11, 13, 17, 19, 23 et 29. L'entier 1 n'est pas premier car il n'a pas deux diviseurs positifs distincts, mais un seul, à savoir lui-même. Il existe une infinité de nombres premiers. En complétant une grille de taille 10 × 10 avec les 100 premiers entiers naturels non nuls, et en rayant ceux qui ne sont pas premiers, on obtient les nombres premiers appartenant à {1, …, 100} par un procédé appelé un crible d'Ératosthène, du nom du savant grec qui l'inventa.

Nombres pairs et impairs |

Les entiers naturels peuvent être divisés en deux catégories : les pairs et les impairs.

Un entier n{displaystyle n} pair est un multiple de 2 et peut par conséquent s'écrire n=2k{displaystyle n=2,k}, avec k∈N{displaystyle kin mathbb {N} }. Un nombre n{displaystyle n} impair n'est pas multiple de 2 et peut s'écrire n=2k+1{displaystyle n=2,k+1}, avec k∈N{displaystyle kin mathbb {N} }.

On montre que tout entier est soit pair soit impair, et ce pour un unique k{displaystyle k} : on note ∀n∈N∃!k∈N(n=2k∨n=2k+1){displaystyle forall nin mathbb {N} quad exists !kin mathbb {N} quad left(n=2,klor n=2,k+1right)}.

Les six premiers entiers pairs sont 0, 2, 4, 6, 8 et 10.
Les six premiers entiers impairs sont 1, 3, 5, 7, 9 et 11.

Notes et références |

Voir aussi |

Articles connexes |

Bibliographie |

Mathématiques |

• Daniel Perrin, « Cours numéro 6 : Arithmétique et cryptographie », sur Département de mathématiques d'Orsay, 2010


• Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]

Philosophie |

• 
  Gottlob Frege, Les Fondements de l'arithmétique, 1884


• 
  Richard Dedekind, Was sind und was sollen die Zahlen?, 1888


• 
  Edmund Husserl, Philosophie de l'arithmétique (en), 1891

v · m Notion de nombre
Ensembles usuels	.mw-parser-output .sep-liste{font-weight:bold} Entier naturel (N{displaystyle scriptstyle mathbb {N} }) · Entier relatif (Z{displaystyle scriptstyle mathbb {Z} }) · Nombre décimal (D{displaystyle scriptstyle mathbb {D} }) · Nombre rationnel (Q{displaystyle scriptstyle mathbb {Q} }) · Nombre réel (R{displaystyle scriptstyle mathbb {R} }) · Nombre complexe (C{displaystyle scriptstyle mathbb {C} })
Extensions	Quaternion (H{displaystyle scriptstyle mathbb {H} }) · Octonion (O{displaystyle scriptstyle mathbb {O} }) · Sédénion (S{displaystyle scriptstyle mathbb {S} }) · Nombre complexe déployé · Tessarine · Nombre bicomplexe (C2{displaystyle scriptstyle mathbb {C} _{2}}) · Nombre multicomplexe (Cn{displaystyle scriptstyle mathbb {C} _{n}} · MCn{displaystyle scriptstyle {mathcal {M}}mathbb {C} _{n}}) · Biquaternion · Coquaternion · Quaternion hyperbolique · Octonion déployé · Nombre hypercomplexe · Nombre p-adique (Qp{displaystyle scriptstyle mathbb {Q} _{p}}) · Nombre hyperréel · Nombre superréel · Nombre dual · Droite réelle achevée · Nombre cardinal · Nombre ordinal · Nombre surréel · Nombre pseudo-réel
Propriétés particulières	Parité · Nombre premier · Nombre composé · Nombre figuré · Nombre parfait · Nombre positif · Nombre négatif · Fraction dyadique · Nombre irrationnel · Nombre algébrique · Nombre transcendant · Nombre imaginaire pur · Nombre de Liouville · Période · Nombre normal · Nombre univers · Nombre constructible · Nombre réel calculable · Nombre transfini · Infiniment petit
Exemples	Pi (π) · Racine carrée de deux (2{displaystyle scriptstyle {sqrt {2}}}) · Nombre d’or (φ) · Zéro (0) · Unité imaginaire (i) · Constante de Neper (e) · Aleph-zéro (ℵ0) · Table de constantes mathématiques
Articles liés	Chiffre · Numération · Fraction · Opération · Calcul · Algèbre · Arithmétique · Suite d'entiers · Infini (∞) · Chiffre significatif

• Portail de l’arithmétique et de la théorie des nombres